Kalman Filters for Orbit Trajectory Estimation

Instructions:

This was a team project where we were tasked with analyzing the performance of the proposed autonomous-navigation system and ultimately determine whether it is suitable for the company’s mission to Bennu. We did so using numerical simulations of (i) the spacecraft orbital motion about the asteroid, (ii) landmark-based line-of-sight measurements, and (iii) the navigation filter itself.

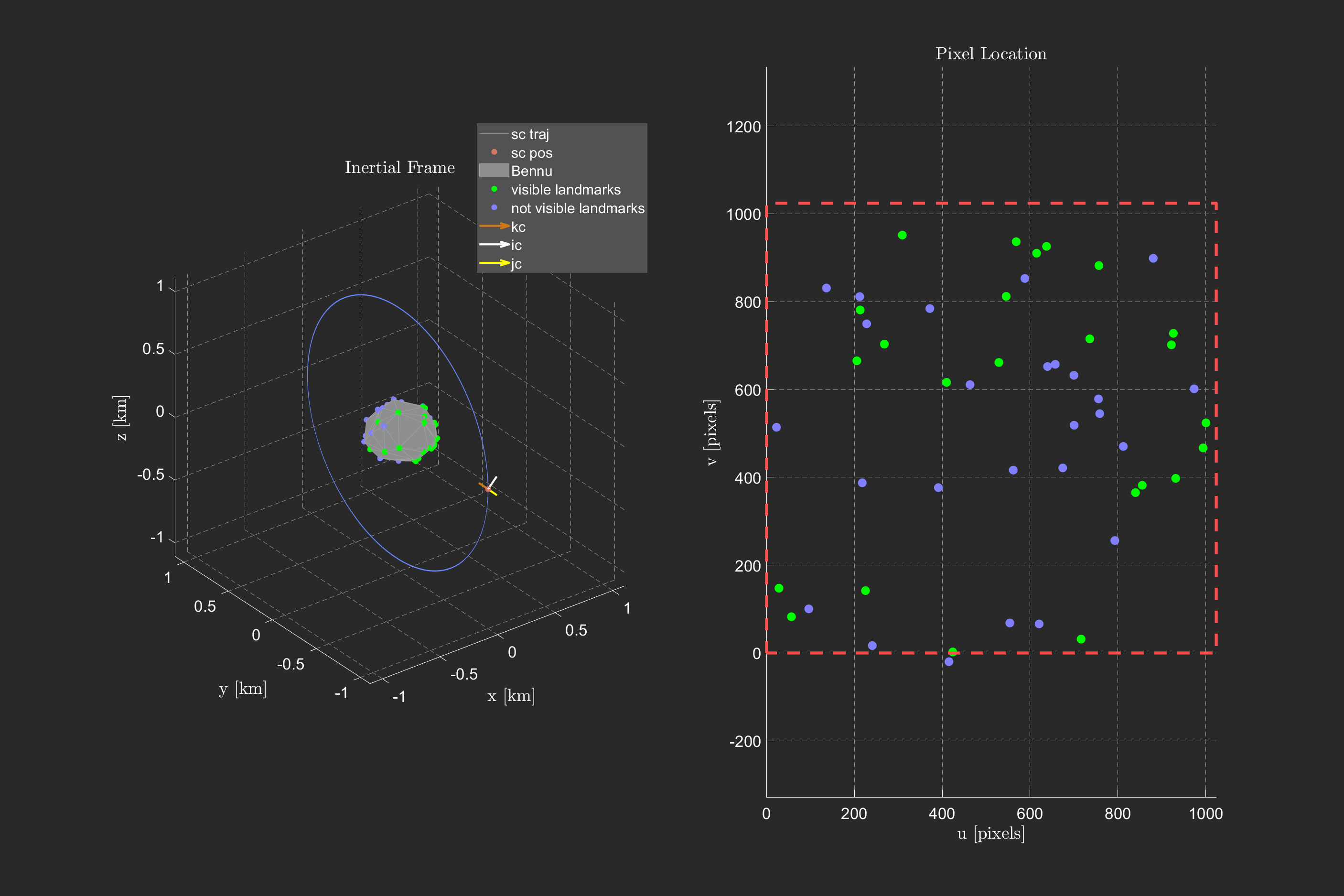
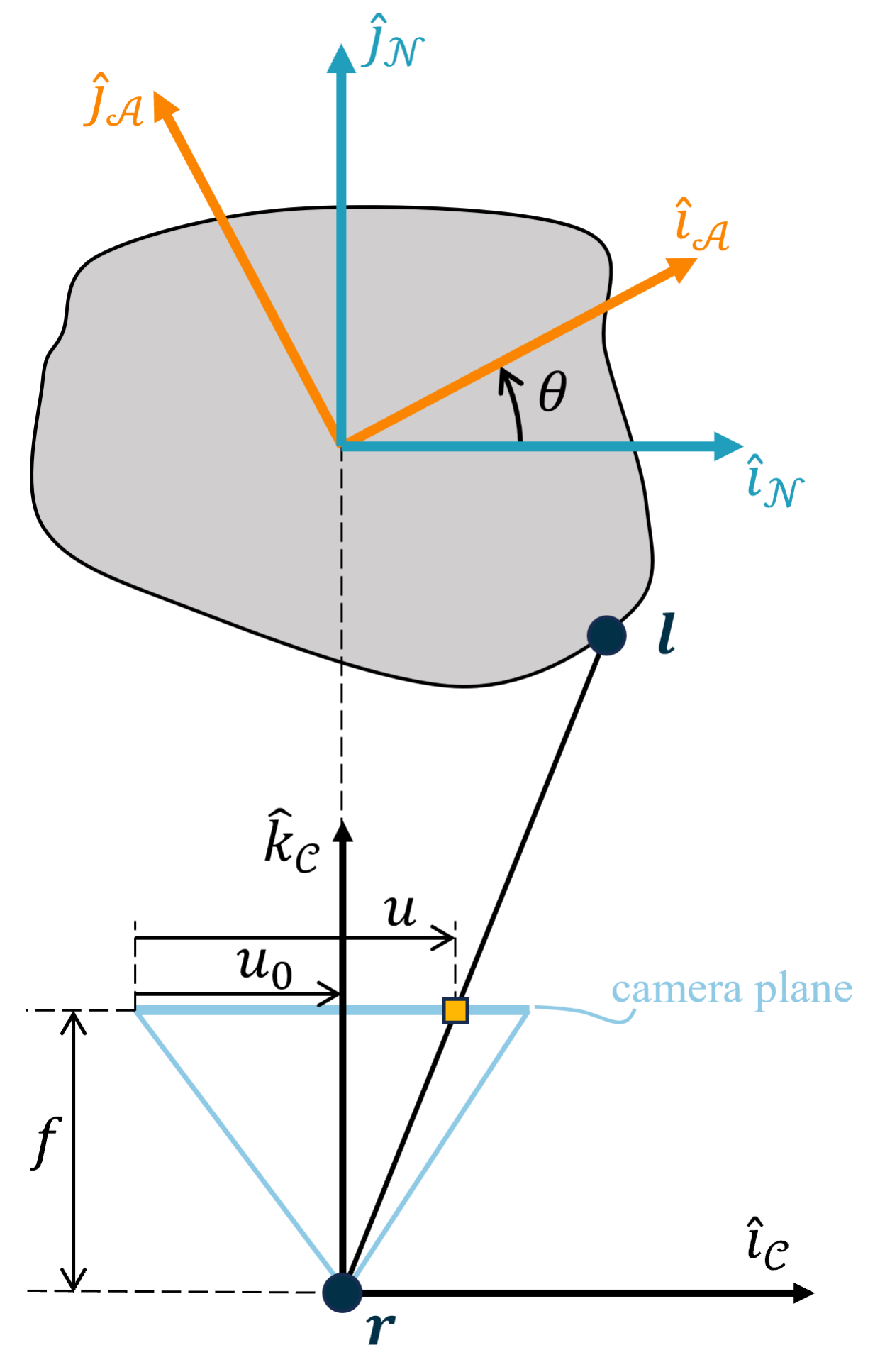
We utilized a pinhole-camera model to convert pixel locations on a focal plane to extract the focal point location, which we assumed was at the center of the spacecraft.

Using both non-linear and linearized two-body gravity models, we propagated perturbations and created trajectorys to estimate the spacecraft state at certain timesteps. We utilized both Linear, Extended, and Unscented kalman filters to update the correction using the measured information.

Given the high non-linearity of orbit trajectories, the linear KF proved to be unstable when measurement and process noise was introduced into the system. However, the extended KF and unscented KF utilized a nominal trajectory that was updated according to each step’s new state estimate. This allowed the EKF and UKF to track and estimate the actual trajectory with minimal error.

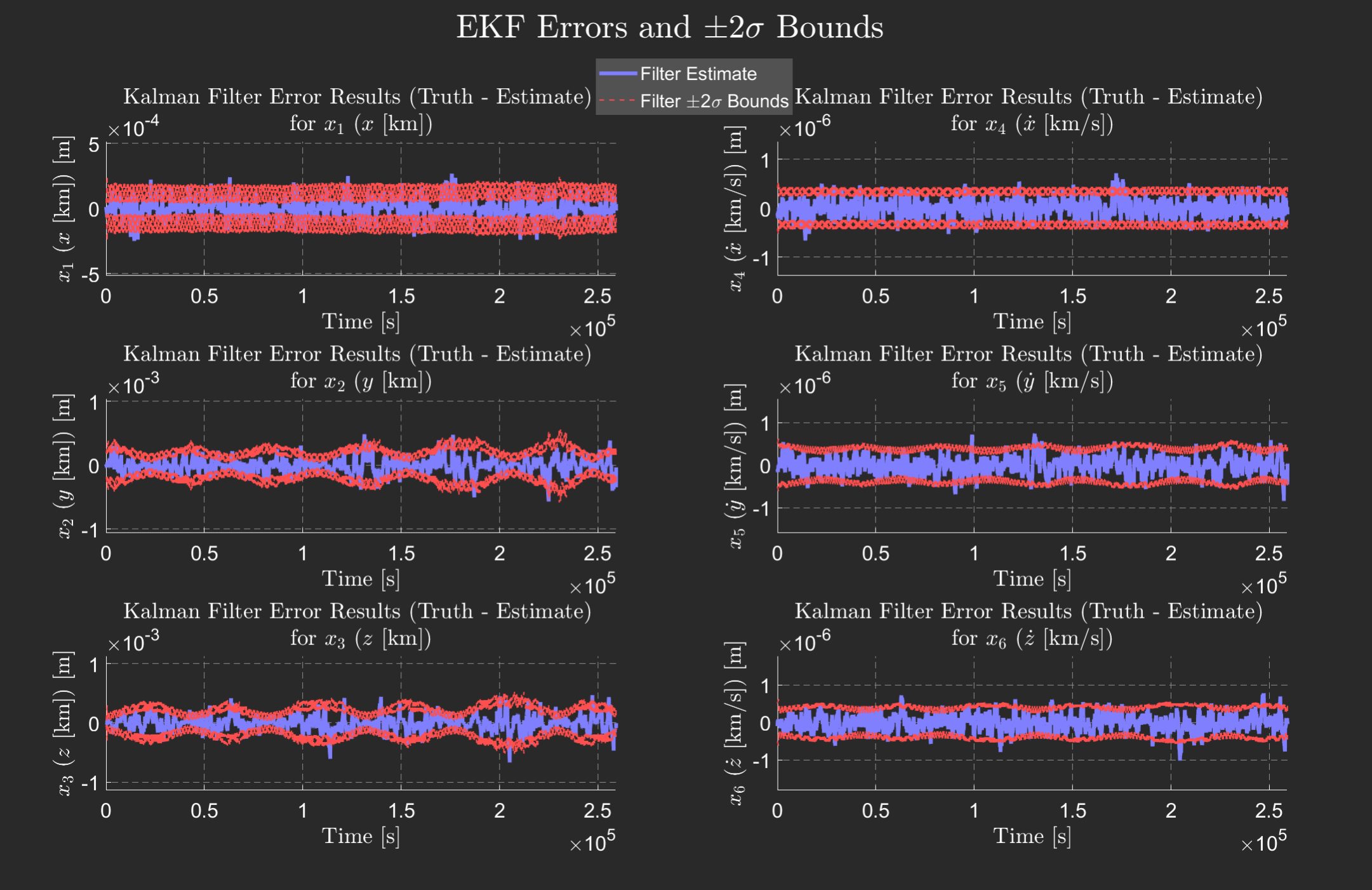
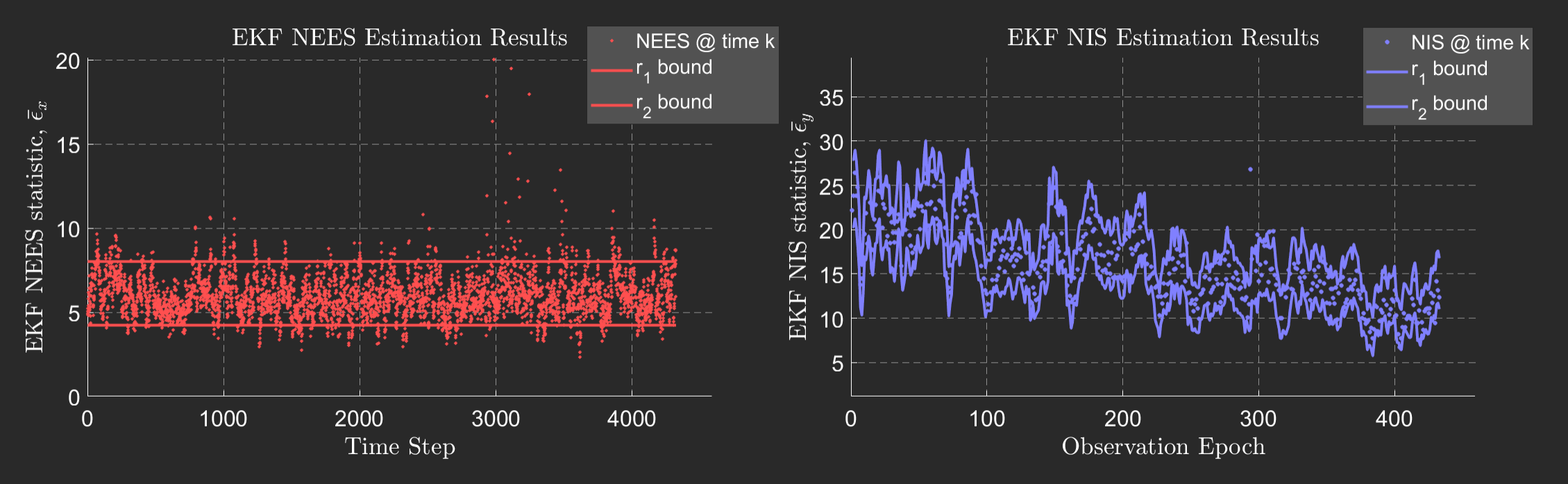
In the presence of measurement and process noise, Q tuning was performed to adjust the error uncertainy plus\minus 2-sigma bounds to capture the state estimate very well. Normalized Error Estimation Squared (NEES) and Normalized Innovation Squared (NIS) testing was additionally performed to ensure the filters were consistent and producing quality estimates.